Verification of Aberrational Correction on Swarm

This document justifies the correctness of the aberrational correction of the Swarm attitude data from the Star Tracker (STR).

The three STR Camera Head Units (CHU) are mounted nearly perfectly perpendicular to each other. This implies, that if the aberrational correction of one head, CHU_i, is perpendicular to the boresight of another head, CHU_j, (and hence not visible in the inter-boresight angle, IBA, between the heads i and j) then it is parallel to the boresight of the third head, CHU_k, and thus affects the IBA between heads i and k in full.

To further justify the correctness of the aberrational correction (AC), a series of verifications have been performed for various local times and various seasons. Below, a number of plots showing the effect of the AC is given. The plots visualize the effect of the AC for the three pairs of CHU's both as projections onto the corresponding plane of the CHU's and as IBA's of the CHU's. The AC effect is computed as the difference between the un-corrected attitude information provided in the Level 0 data (raw) and the corrected attitude information (corr - extracted from within the Level 1b Processor). These data are available as MATLAB save files containing the following variables:

Name		Type	Description
t		nx1 double	Time instants of data. MATLAB times (datenum).
pos		nx3 double	Satellite positions, ITRF, Cartesian, metres
chu		1x3 struct	Structures holding information for the three heads
	q_raw	nx4 double	Uncorrected attitude (quaternion), from Level 0
	valid	nx1 logical	True, if attitude information is valid
	residual	nx1 double	Residual of attitude solution compared to on-board star catalogue, arc-seconds
	q_corr	nx4 double	Corrected attitude (quaternion), from Level 1b processing

The following plots show (click for larger images or here for all plots in full size):

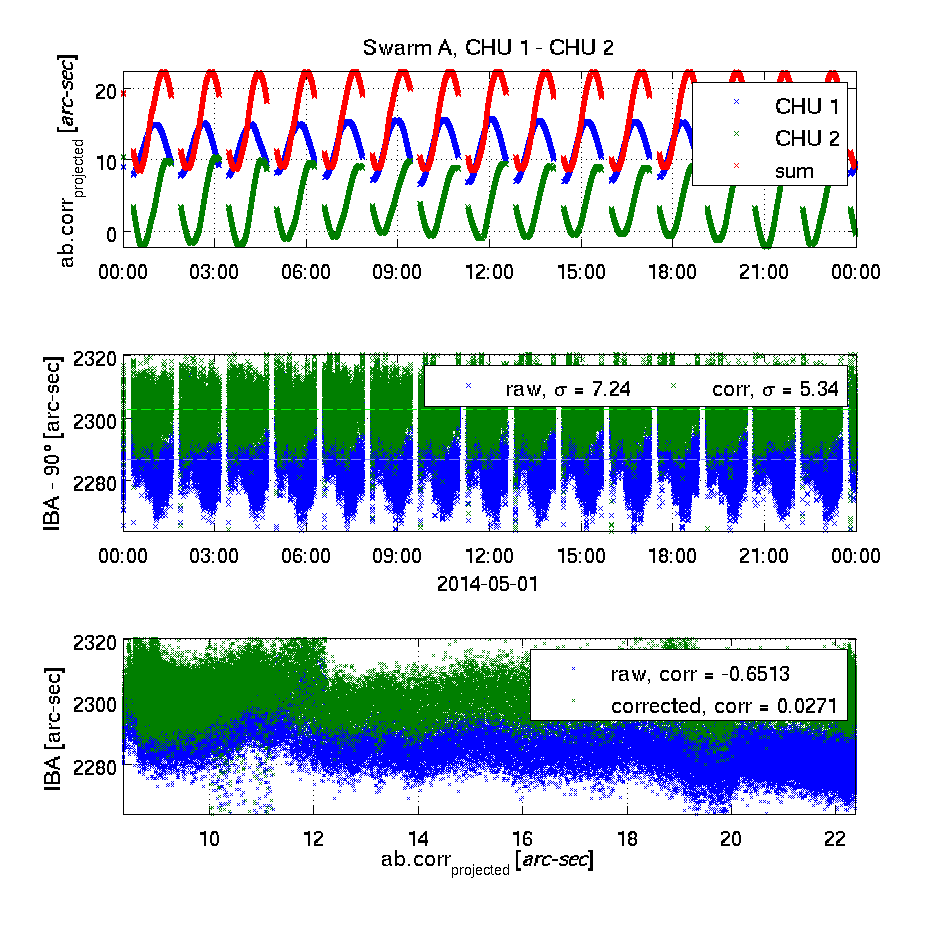
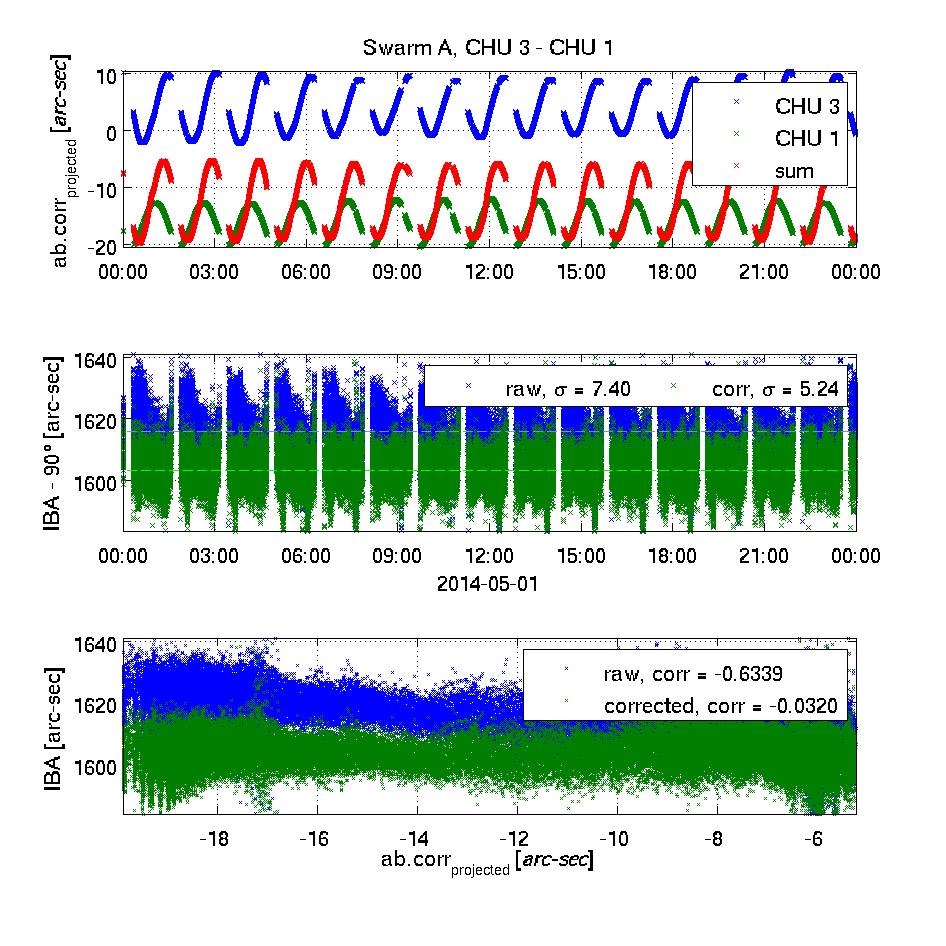
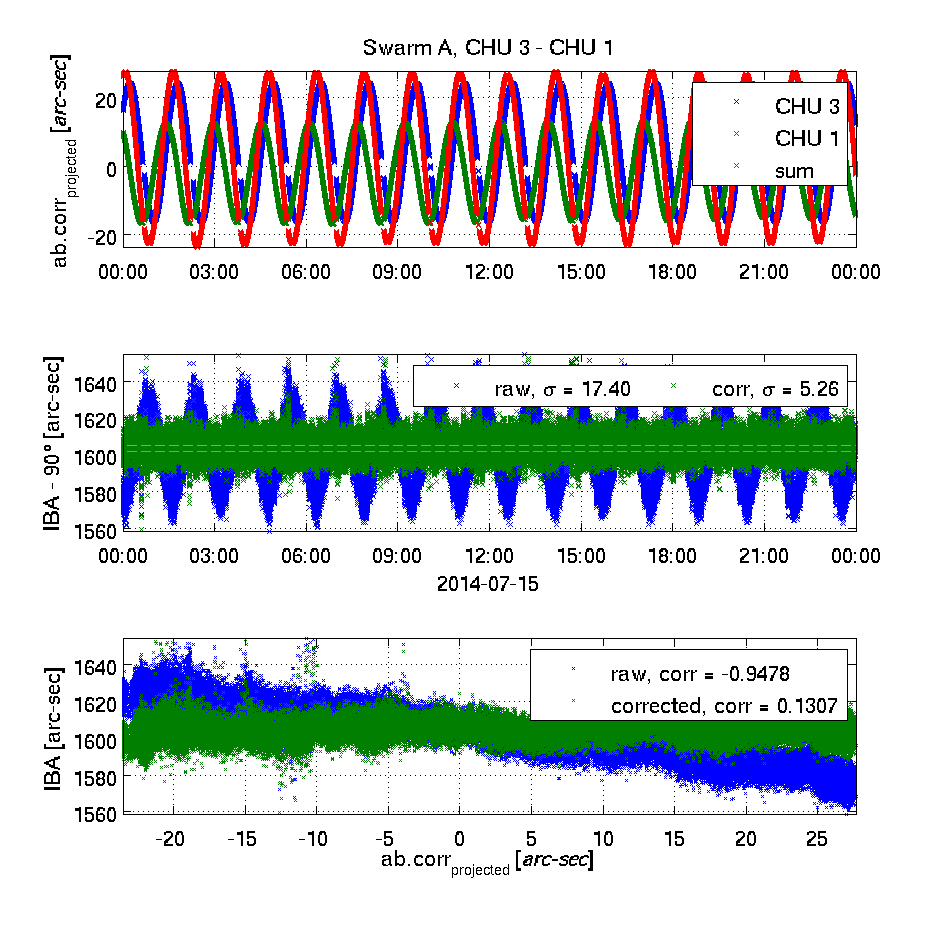
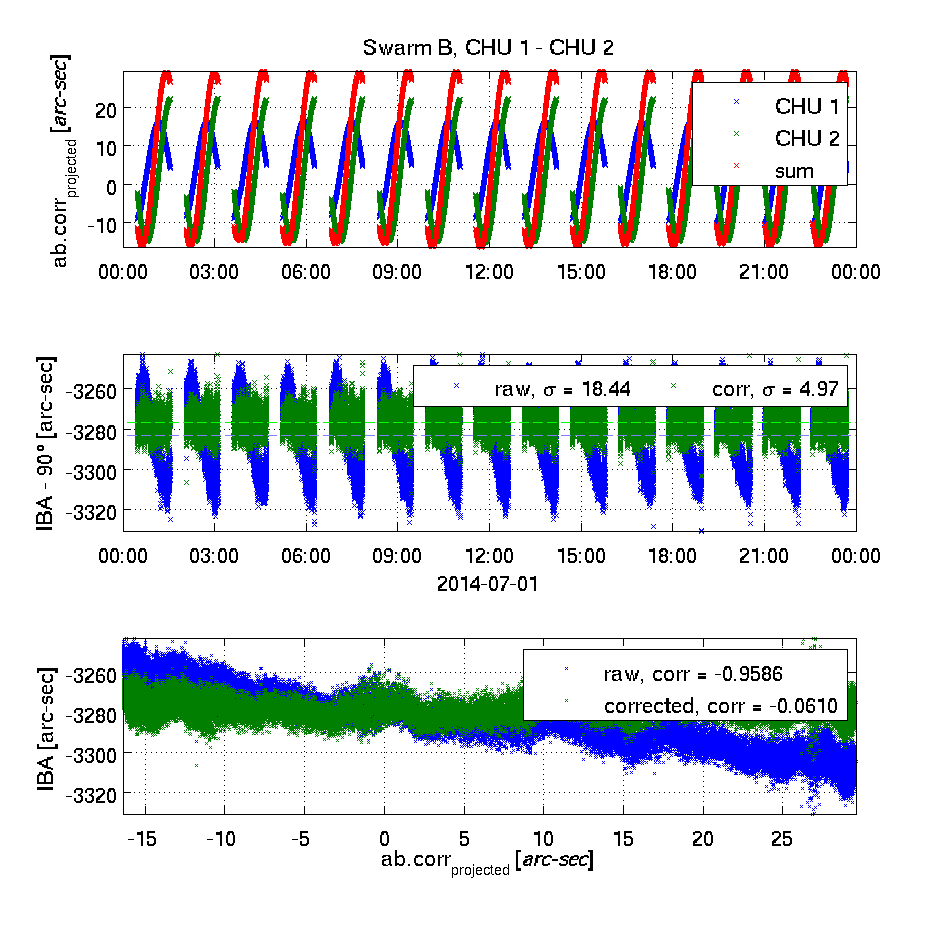
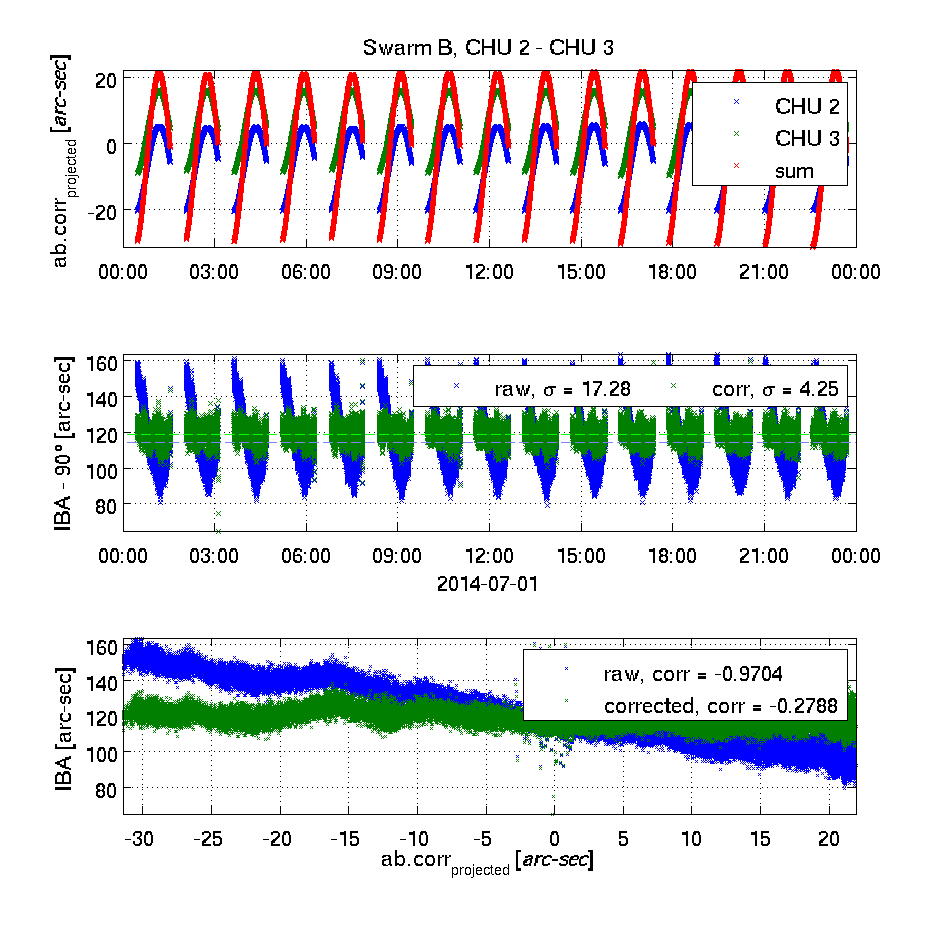
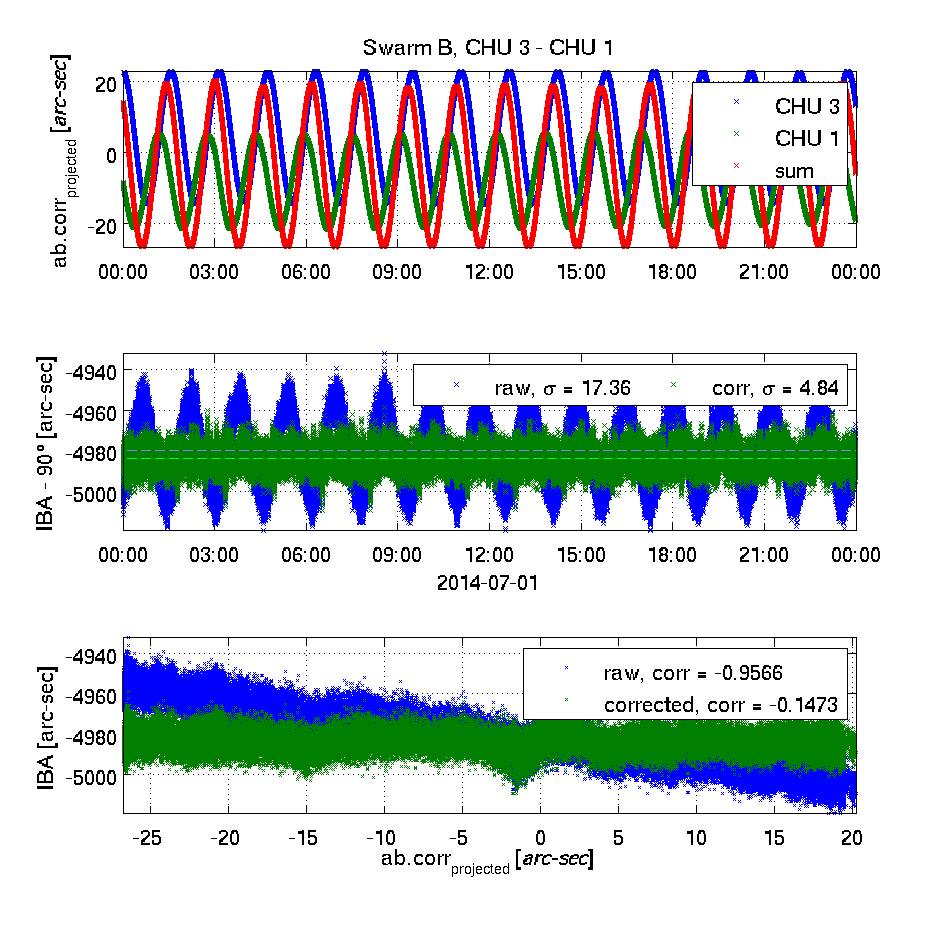
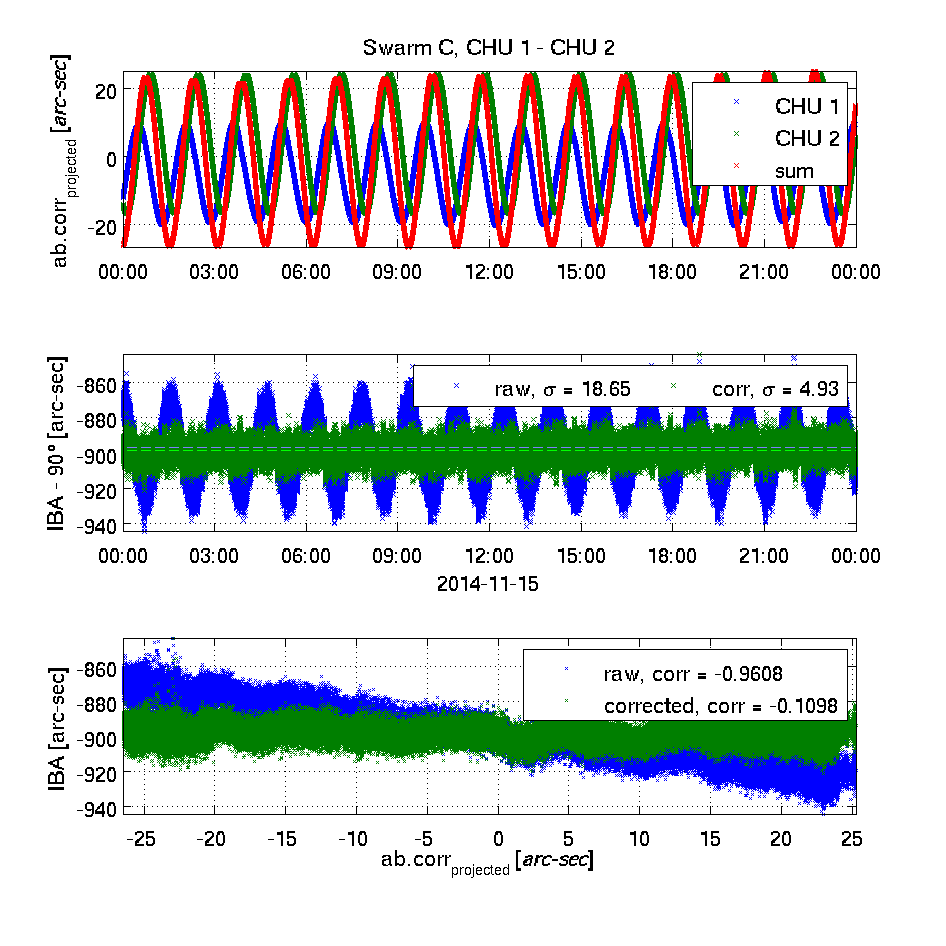
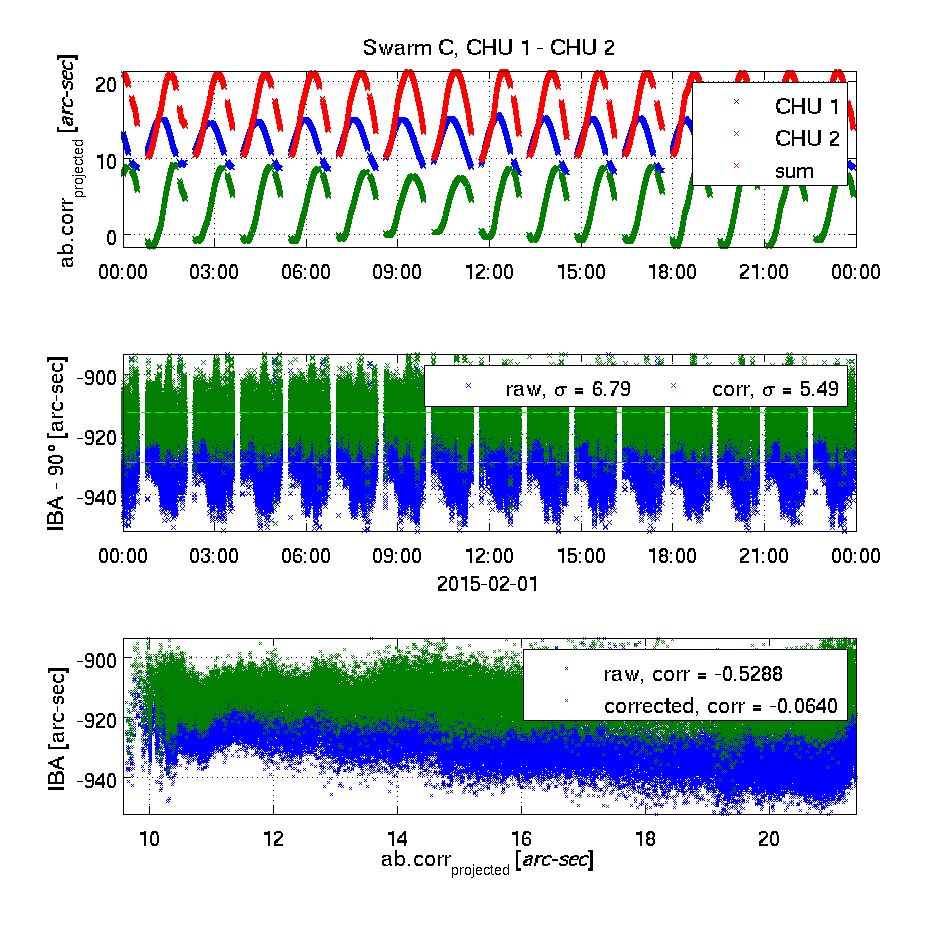
The top plot shows the effect of the Level 1b aberrational correction projected into the plane of the two camera heads being investigated - in blue and green respectively. Positive values indicate a correction away from the other head's boresight. In red, the sum of the two is plotted. The unit is approximated arc-seconds.

The middle plot shows the inter-boresight angles (IBA - 90°) for the uncorrected (raw, in blue) and the corrected (in green) attitude information. The mean values are shown as dashed lines (in cyan and light green respectively); the weighted standard deviations are given in the legends.

The bottom plot shows the correlation between the un-corrected and corrected IBA's and the sum of the projected aberrational corrections (the red curve in the top plot) - the correlation coefficients are given.

This high correlation between un-corrected IBA's and sums of projected aberrational corrections as well as the lack of correlation for the corrected IBA's clearly demonstrates the correctness of the applied aberrational correction.

Swarm Alpha, 2014-05-01, data

Swarm Alpha, 2014-07-15, data

Swarm Bravo, 2014-07-01, data

Swarm Charlie, 2014-11-15, data

Swarm Charlie, 2015-02-01, data